字符串匹配 - KMP 速通 · 一个技术宅的碎碎念

Table of Contents

字符串匹配是个常见的问题。其中经典的 KMP 算法又是一个不好理解且容易遗忘的算法。本文简要介绍与字符串匹配相关的几个算法，使用 Swift 实现来解决：

28. Find the Index of the First Occurrence in a String

问题抽象 #

给定两个字符串：S 是主串，P 是模式串。在 S 中查找等于 P 的子串（substring，连续的序列）。其中 S 长度 n，P 长度 m。

暴力算法 (Brute-Force) #

最朴素的算法，复杂度 O(n * m)

func bruteForce(_ haystack: String, _ needle: String) -> Int {
    let text = haystack.map { String($0) }
    let pattern = needle.map { String($0) }
    let n = text.count, m = pattern.count
    guard n >= m else { return -1 }
    var ans = [Int]()
    for i in 0...n-m {
        var check = true
        for j in 0..<m {
            guard text[i+j] == pattern[j] else {
                check = false
                break
            }
        }
        if check {
            ans.append(i)
        }
    }
    return ans.count > 0 ? ans[0] : -1
}

KMP 算法 #

由 Knuth & Morris & Pratt 提出，时间复杂度 O(n + m)

LPS 数组 #

LPS, longest proper prefix which is also a suffix.¹

注意，这里的 proper prefix，是指不包括字符串本身的前缀（如果包含，那么最长的前缀和后缀肯定是自身了）。

数学描述是：

$$ LPS[i] = max \lbrace \space k \space | \space P[0..<k] = P[(i-k+1)…i] \space \rbrace $$

$ LPS[i] $ 表示 $ P[0…i] $ 这个子字符串中，等长前缀与后缀相同的最大的长度 $k$。那么，显然 $ LPS[0] = 0 $。

我们称 P[0..<k] 或者 P[(i-k+1)…i] 这种即是前缀又是后缀的子串，为 P 的 border。²

求解 LPS 的过程其实是 DP (Dynamic Programming)，时间复杂度 O(m)。

参考后续代码实现。

有时，也会见到 next 数组或者 PMT (Partial Matching Table) 表，它其实和 LPS 是一回事，只不过存在一个简单的转换关系：

$$ LPS[i] = next[i] + 1, i \in [0,m] $$

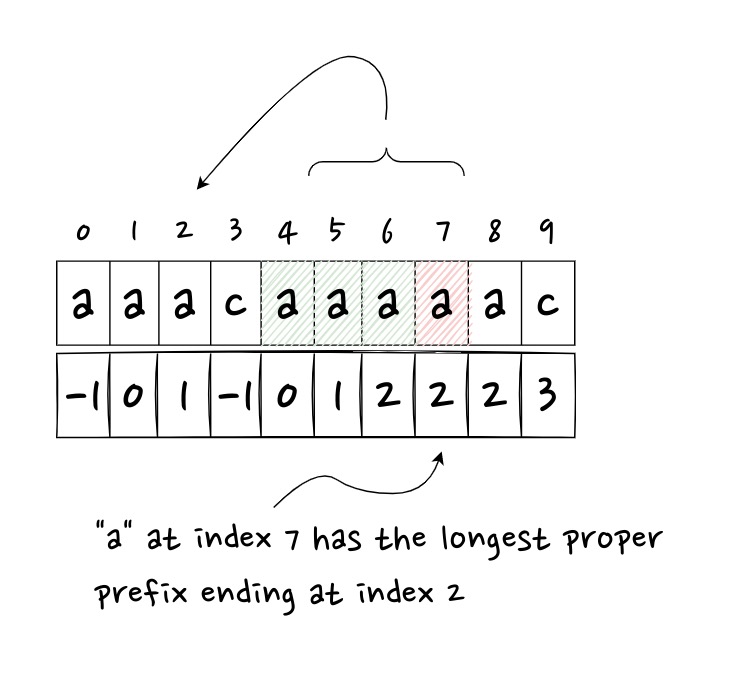
上图就是 next 数组，对应的 LPS 数组就是 $ [0, 1, 2, 0, 1, 2, 3, 3, 3, 4] $

匹配 #

暴力算法中，在遇到不匹配的情况：$ S[i] \not = P[j] $ 时，会将主串向后移动一位，模式串从 0 重头开始匹配。

KMP 算法中，这时匹配串会从 $ LPS[j-1] $ 开始匹配，主串不动。也相当于暴力算法中主串移动了 $ (j - LPS[j-1]) $ 位。

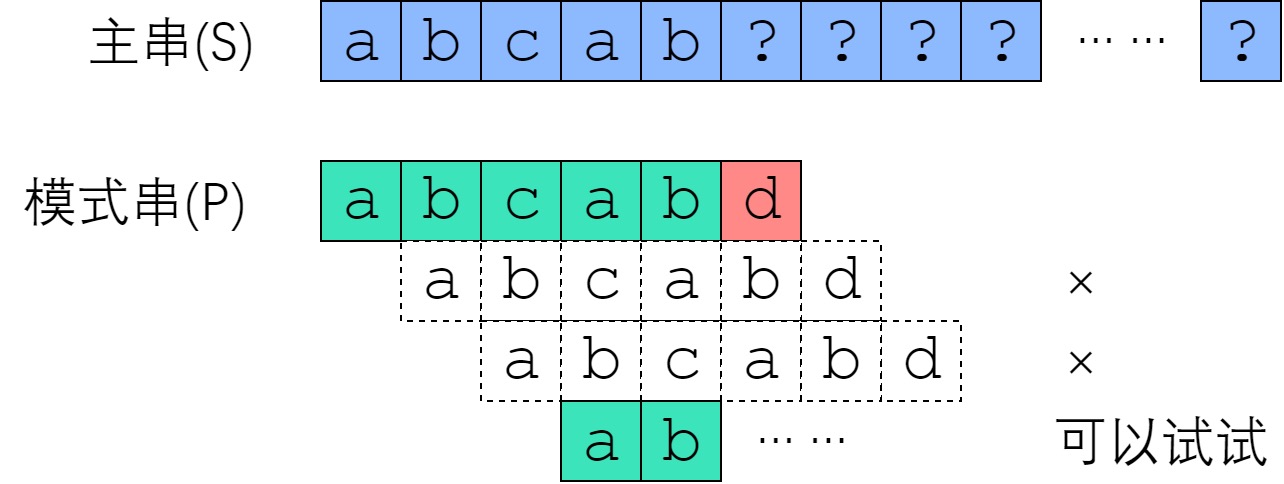
为什么？

因为根据定义，子串 $ P[0..<j] $ 的最长前缀和后缀相同的长度是 $ LPS[j-1] $。

如上图所示，将 $ j $ 向后移动一位，从头开始匹配，如果子串中的 $ abca $ 能匹配主串中的 $ bcab $，也就意味着能匹配子串自身的后四位，这样就与求解的 $ LPS[j-1] $ 不符。

完整的实现如下：

func kmp(_ haystack: String, _ needle: String) -> Int {
    let LPS = { (str: String) -> [Int] in
        let pattern = str.map { String($0) }
        let m = pattern.count
        guard m > 0 else { return [] }
        var lps = [Int](repeating: 0, count: m)
        var i = 1, j = 0
        while i < m {
            if pattern[i] == pattern[j] {
                j += 1
                lps[i] = j
                i += 1
            } else {
                if j > 0 {
                    j = lps[j-1]
                } else {
                    lps[i] = 0
                    i += 1
                }
            }
        }
        return lps
    }(needle)

    print(LPS)

    let text = haystack.map { String($0) }
    let pattern = needle.map { String($0) }
    let n = text.count, m = pattern.count
    guard n >= m else { return -1 }
    var ans = [Int]()
    var i = 0, j = 0
    while i < n {
        if text[i] == pattern[j] {
            i += 1
            j += 1

            if j == m {
                ans.append(i - j)
                j = LPS[j-1]
            }
        } else {
            if j > 0 {
                j = LPS[j-1]
            } else {
                i += 1
            }
        }

    }
    return ans.count > 0 ? ans[0] : -1
}

有意思的是，求解 LPS 的过程和匹配的过程非常像！

BM 算法 #

Boyer-Moore 算法是于 1977 年由德克萨斯大学的 Robert S. Boyer 教授和 J Strother Moore 教授提出。

Sunday 算法 #

从 BM 算法改进而来。由 Daniel M.Sunday 于 1990 年提出。³

Z 算法 #

也叫 扩展 KMP 算法。⁴

与 LPS 类似，Z 算法的核心是 Z 函数，或者叫 Z 数组：

$$ Z[i] = max \lbrace \space k \space | \space P[0..<k] = P[i..<i+k] \space \rbrace $$

$ Z[i] $ 表示以 $i$ 开头的子串与模式串本身的最长公共前缀 (LCP) 的长度。

这里定义区间 $ [i..<i+Z[i]] $ 为一个 Z-Box，显然它也是整个字符串的一个前缀。

Z 函数有很多用处，具体到字符串匹配中，我们可以将 P 与 S 组合起来：

$ S^{\prime} = P + ‘\$’ + S $

其中 $\$$ 是在 S 和 P 中都不出现的字符。

接下来求解 $ S^{\prime} $ 的 Z 函数，然后对于所有 Z 数组中的值，只要等于 P 的长度，即为匹配！

func zAlgorithm(_ haystack: String, _ needle: String) -> Int {
    let Z = { (str: String) -> [Int] in
        let s = str.map { String($0) }
        let n = str.count
        var z = [Int](repeating: 0, count: n)
        var l = 0, r = 0
        for i in 1..<n {
            if z[i - l] < r - i + 1 {
                z[i] = z[i - l]
            } else {
                z[i] = max(r - i + 1, 0)
                while i + z[i] < n && s[z[i]] == s[i + z[i]] {
                    z[i] += 1
                }
                l = i
                r = i + z[i] - 1
            }
        }
        return z
    }(needle + "$" + haystack)

    print(Z)

    let n = haystack.count, m = needle.count
    guard n >= m else { return -1 }
    var ans = [Int]()
    for i in m+1..<n+m+1 {
        if Z[i] == m {
            ans.append(i - m - 1)
        }
    }
    return ans.count > 0 ? ans[0] : -1
}

这个 Z 函数的求解算法，不太好理解 😭