树的结构与算法之二：构造

Table of Contents

上文介绍了树的遍历，这次说一下如何从数组构造树结构。

层次构造 #

一般测试数据的输入是数组，我们需要将数组转换成树结构。同时，为了便于输出验证，也需要将树再转回数组。

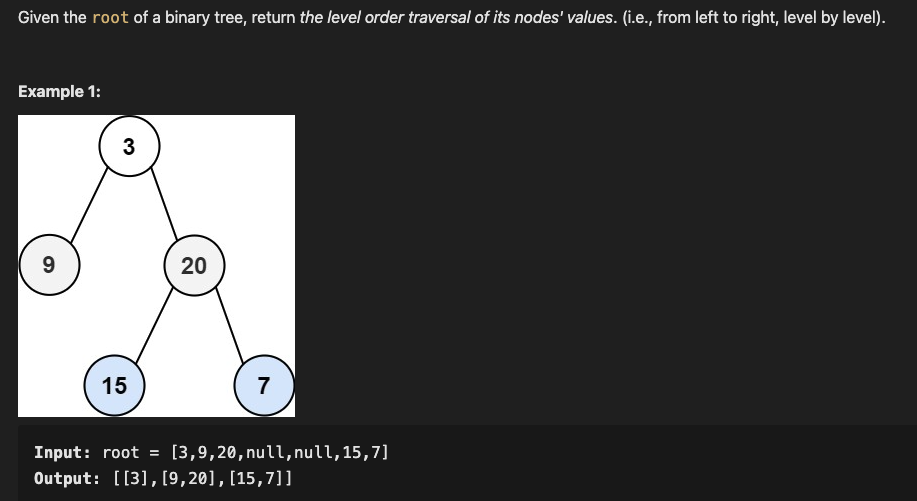
来源：102. Binary Tree Level Order Traversal

其实就是层次遍历及其逆向构造树的过程。

public extension TreeNode {
    func array() -> [Int?] {
        var ans: [Int?] = []
        var queue: [TreeNode?] = [self]
        while !queue.isEmpty {
            if let node = queue.removeFirst() {
                ans.append(node.val)
                queue.append(node.left)
                queue.append(node.right)
            } else {
                ans.append(nil)
            }
        }
        // remove nils at last
        while ans.last == nil {
            ans.removeLast()
        }
        return ans
    }

    // TODO: to be optimized
    static func arrayToTree(_ nums: [Int?]) -> TreeNode? {
        guard nums.count > 0 else { return nil }
        guard let rootVal = nums[0] else { return nil }
        let root = TreeNode(rootVal)
        var queue: [TreeNode?] = [root]
        var i = 1
        let sz = nums.count
        while !queue.isEmpty && i < sz {
            let node = queue.removeFirst()
            if let val = nums[i] {
                let left = TreeNode(val)
                node?.left = left
                queue.append(left)
            }
            i += 1
            if i >= sz {
                break
            }
            if let val = nums[i] {
                let right = TreeNode(val)
                node?.right = right
                queue.append(right)
            }
            i += 1
        }
        return root
    }
}

这个构造过程过于朴素，需要后续优化下 🥸

Update #

一种更 Swifter 的写法

func array() -> [Int?] {
    var result = [Int?]()
    var tree: [TreeNode?] = [self]
    while !tree.isEmpty {
        guard tree.compactMap({ $0 }).count > 0 else { break }
        result.append(contentsOf: tree.map { $0?.val })
        tree = tree.compactMap { $0 }.flatMap { [$0?.left, $0?.right] }
    }
    return result
}

前序与中序构造 #

105. Construct Binary Tree from Preorder and Inorder Traversal

树的结构是递归的，所以大部分与树有关的问题，都是可以使用递归转化成子问题来求解。

前序是 根-左-右 的结构，而中序是 左-根-右，所以：

前序的第一位一定是根
根将中序分成了左子树中序和右子树中序
树的前序和中序长度一样，同样左右子树的前序和中序，长度也是一样的。
这样问题就转换成了：
- 确定根节点
- 分解成左子树和右子树两个子问题
- 递归调用本身

extension Solution {
    func buildTree(pre preorder: [Int], _ inorder: [Int]) -> TreeNode? {
        let n = preorder.count
        guard n > 0 else { return nil }
        let root = TreeNode(preorder[0])
        guard let rootIdx = inorder.firstIndex(of: root.val) else { return nil }
        if rootIdx > 0 {
            root.left = buildTree(pre: Array(preorder[1...rootIdx]), Array(inorder[0..<rootIdx]))
        }
        root.right = buildTree(pre: Array(preorder[rootIdx+1..<n]), Array(inorder[rootIdx+1..<n]))
        return root
    }
}

中序与后序构造 #

106. Construct Binary Tree from Inorder and Postorder Traversal

思路同上：

后序是 左-右-根，所以最后一位是根

extension Solution {
    func buildTree(_ inorder: [Int], post postorder: [Int]) -> TreeNode? {
        let n = inorder.count
        guard n > 0 else { return nil }
        let root = TreeNode(postorder[n-1])
        guard let rootIdx = inorder.firstIndex(of: root.val) else { return nil }
        if rootIdx > 0 {
            root.left = buildTree(Array(inorder[0..<rootIdx]), post: Array(postorder[0..<rootIdx]))
        }
        root.right = buildTree(Array(inorder[rootIdx+1..<n]), post: Array(postorder[rootIdx..<n-1]))
        return root
    }
}